差集め算　その3

こんにちは。
差集め算の続きです！
前回はパターン1でしたので、今回はパターン2を。
｜問題｜
K君は文房具屋さんで鉛筆を買うつもりでお金を持っていきました。鉛筆Aを12本買うと60円余ります。鉛筆Bを10本買おうとすると100円足りません。鉛筆Aと鉛筆Bの値段の差が30円のとき、K君の持っていたお金はいくらですか。
｜解法｜
まずは、線分図を書いてみましょう。
A12本は持っているお金より60円少ない。
B10本は持っているお金より100円多い。

次に「個数」を合わせます。
前回と同様、考え方は2通りありますね。
1.　Aを2本減らす
2.　Bを2本増やす
今回は「1.」の方でやってみます。
Aを2本減らすと、線分図は次のようになります。

ここで3つの関係を思い出しましょう！
代金の差＝1つずつの差×個数
この問題ではAとBの値段の差は30円と書いてあるので、
10本ずつ買ったときの代金の差は、
30円×10本ずつ＝300円
線分図で言うと、次の部分です。

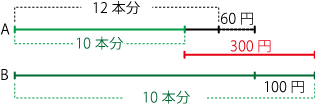
さて、ここで次の赤い部分に注目です。

この赤い部分(300円－100円ー60円＝140円)、
A2本分の代金なのがわかりますか？
つまり、A1本を求めると、　140円÷2本＝70円…A1本
ちなみにB1本はAより30円高いはずなので、　70円＋30円＝100円…B1本　です。
問題ではK君が持っていたお金なので、
Aで考えると、12本分と60円、
つまり、　70円×12本＋60円＝900円…持っていたお金　となります。
「2.」でやっても同じこと。
12本分ずつ買うと、30円×12本＝360円差となり、B2本分が200円となるはずです。
これが差集め算のパターン2の解き方です。
パターン1とパターン2の見分け方は、
パターン1　：　1つずつの値段がわかっていて、本数がわからない場合。
パターン2　：　本数がわかっていて、1つずつの値段がわからない場合。
と逆の関係になっています。
例外の問題もありますが、
どちらも中受では重要なので、しっかりと覚え、練習しておきましょう！