規則性の問題

こんばんは。
今日も一日が終了しました。
6年生の算数でやった規則性の問題。
規則性というのは、ちょっとでも問題が変わると、
規則性自体が変わってしまうので、なかなか応用力を必要とします。
しかし、まずは絶対に知っていなければならないことをきちんとできるようにしておきましょう。
たとえば、
等差数列(公式は分かっていますか？)、
約数・倍数(公約数や公倍数をサクッと言えますか？)
周期算(わり算をして何が出たのか分かりますか？)
特殊な数列(100＝1＋2＋…＋13＋9がすぐに思いつきますか？)
その他(1から始まる奇数の和は「個数×個数」を使いこなせますか？)
などです。
基本的な計算方法がしっかりとわかっていないと、
答えを出すことが難しくなってしまうので、まずはそこを確実にしておきましょう。
あとは、いろいろな規則性の問題を解いてみて、
「こんな規則もあるんだ～」という知識を増やしていきましょう。
ポイントは「規則と規則をあわせると、そこにまた規則が生まれる」ということ。
逆に「規則を分解してみると、そこにまた規則が現れる」ということ。
規則性の問題は、どんな問題を解くのにも大切です。
速さの問題で、同じところを何度も往復している時点で、規則性は出てきますし、
場合の数などでも規則性で解けてしまうものもありますし、
計算してみたら、答えに規則性が出てきたりと、
結構、規則性っていろいろなところで活躍できるのです。
頑張って規則性を見つけ出しましょうね。
それではまた明日。
今日の問題
　次の表はある規則によって1から順に数を書き並べたものの一部です。第2行第4列は13です。このことを〔2,4〕＝13と表すことにします。これについて、次の問いに答えなさい。
　
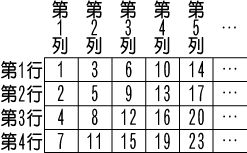
(1)〔3,50〕はいくつですか。
(2)250を記号を用いて表しなさい。
答えを表示⑴196
⑵〔1,64〕