2つの解き方

今日の5年生のRepeat特講(算数)では図形の問題をやりました。
面積の公式は、しっかりと覚えられているようですね。
ちょっと複雑な図形になると、
やはり、手が止まってしまいます。
まずは、問題に書いてある長さや面積を図に書き込むところからはじめ、
面積が求められるところや、長さが求められるところを計算してしまいましょう。
ところで、算数には答えを出す方法が2つあります。
ちょっと難しいかもしれませんが、今日はその話を5年生にしてみました。
一つは、問題に書いてあることでできることをやっていく方法。
もうひとつは答えを出す為に欲しいものを探していく方法です。
前述した「まずは、図形に…」は「できることをやっていく」方法です。
例えば、「K君は20円の品物と30円の品物を買いました。」
と書いてあったらたいていは、　20円+30円=50円　と考えるでしょう。
では、「K君は20円の品物と30円の品物を買いました。100円払った時おつりはいくらでしょう。」
だったらどうしますか？
さっきの考えからすれば、　20円＋30円＝50円
100円払ったのだからおつりは　100円－50円=50円　とすれば答えは出ます。
このやり方は「できることをやっていく方法」です。
でも、このような考え方もできます。
「出したいのはおつり」　→　「おつりを出すには使ったお金と払ったお金がわかればいい」
→　「払ったお金は100円とわかっている」　→　「使ったお金がわかればいい」
→　「使ったお金は20円と30円とわかっている」
なので、逆から計算していくと、
20円＋30円＝50円　100円－50円＝50円
これが「答えを出す為に欲しいものを探していく方法」です。
式としては同じになっていますが、
「できることをやっていく方法」と「欲しいものを順に出していく方法」の２つの考え方ができると、
算数のレベルアップが期待できますよ。
今日の問題
　次の図の四角形ABCDは長方形です。また、三角形FBCの面積は三角形FDEの面積よりも8cm²大きくなっています。このとき、EDの長さは何cmですか。
　
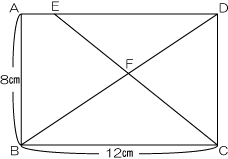
答えを表示10cm