5年生で質問の多かった面積を求める問題。
「次の図は長方形と三角形を組み合わせた図形です。色のついた部分の面積は何cm2ですか。」
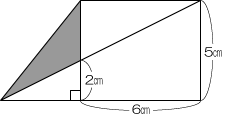
この問題は6年生で「相似」を習ってしまえば簡単にいくのですが、
まだ「相似」を習っていない5年生はどうしても色のついた部分の高さが求まりません。
これを解くために必要なことは、「台形の鉄則」を知っているかどうかです。
1本補助線を付け加えてみましょう。
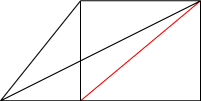
この補助線によって、
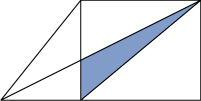
この三角形が求める三角形と同じ面積であることになります。
ということは…
単純に「底辺×高さ÷2」と考えて、
2×6÷2=6cm2 となるのです。
算数では、このように「算数的知識」をしっているかいないかによって、
解ける問題と解けない問題が出てしまいます。
また、10分かけて解く問題が1分で解けてしまったり…。
知識を増やして、手早く解けるようにしていきましょうね。
さて明日はお休みです。
明後日から夏期講習特別期(6年生のみ)が始まります。
時間は9:35~18:15。
初日は国語と算数です。どちらも45分×5コマですから、気合を入れていきましょう。
他の学年は自習室(10:00~18:00)になります。
どんどん参加して下さいね。
それではまた明日。
今日の問題
次のようにあるきまりにしたがって式が並んでいます。このとき、100番目の式の答えはいくつですか。
1+2 3+4 5+6 1+8 3+6 5+4 1+2 3+2 5+4 1+6 3+8 5+6 ……
5
5年生で質問が多かった問題
 未分類
未分類

コメント