冬期講習　4日目-2

5年生の旅人算、結構、苦戦しますね。
なので、今日授業でやった問題を少し解説。
問題
　東町から西町までの道のりは12000mあり、A君は東町から毎分240mの速さで西町に向かい、B君は毎分80m、C君は毎分60mの速さで西町から東町に向かう。A君はC君に出会うとすぐに東町に引き返し、その後、B君に追いつくとまた向きをかえ西町に向かう。3人が午前10時に同時に出発する時、A君は何時何分に西町に到着しますか。
解説
　まずは線分図です。問題に書いてある通りに線分図にしてみます。実はこの作業が一番重要です。
　ポイントとしては、
　　A君とC君が出会う　→　この間にもB君は進んでいるはず。
　　A君がB君に追いつく　→　この間にもC君は進んでいるはず。
　つまり、同じ時間を1つの単位と考えて、必ず全員を進めておくということです。
　下の図では、時間ごとに線分図の色を　赤　青　緑　としています。

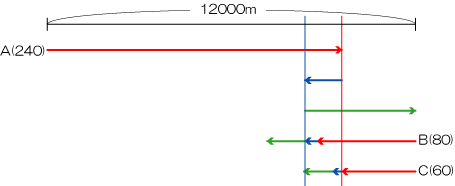
　さて、ここまで書ければ、ほぼこの問題はもらったも同然です。
　A君とC君の和が12000ｍですから、　12000ｍ÷(240+60)＝40分　つまり　赤は40分です。
　すべての赤の部分に40分と書き込むと、速さと時間が出ている部分から道のりを出してしまいましょう。
　240×40＝9600m　・　80×40＝3200m　・　60×40＝2400m

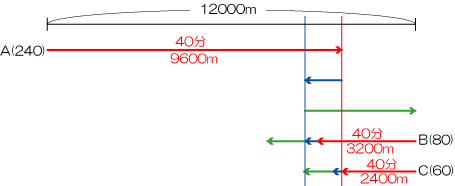
　次にA君がB君に追いつきますから、A君とB君の青い線分図の差は3200－2400＝800ｍ
　追いかけの旅人から　800÷(240－80)＝5分　つまり　青は5分です。
　また、さっきと同じように全ての長さを求めると、

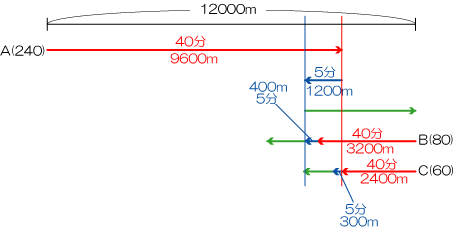
　あとは緑ですが、A君の緑を見てみると、400＋3200＝3600ｍ　と分かります。
　よって、緑の時間は　3600÷240＝15分　です。
　また、同じように緑の線分図を埋めてみましょう。

　
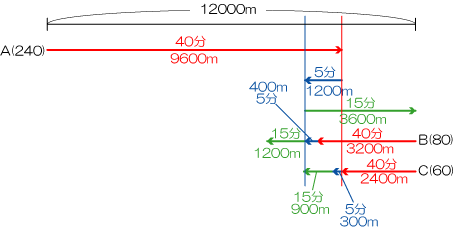
　これですべてが埋まりました。
　答えはというと、午前10時＋40分＋5分＋15分＝午前11時です。
面倒な問題に見えますが、解くこと自体は別に難しいものではありません。
要は線分図が書けるかどうか　が全てのポイントです。
しっかりと復習しておきましょう。